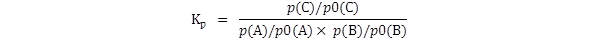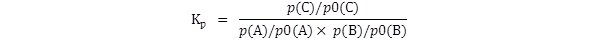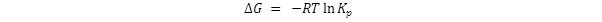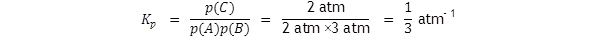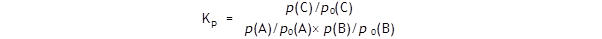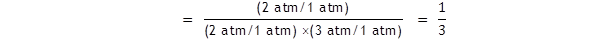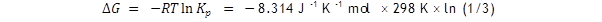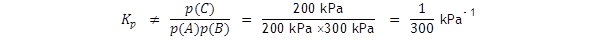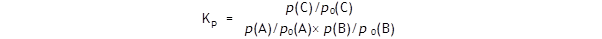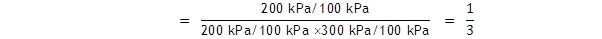Standard pressures and the effect on calculations of K_p.

The new A level specifications for 2015 (first assessment 2017) uniformly use a standard pressure of 100 kN m ^{– 2}  or 100 kPa in their definition of standard states. This replaces the value of 1 atm which has been used for a very long time. This decision is not without a knock-on effect in thermodynamic calculations, especially on how equilibrium constants should be expressed. Edexcel, OCR, Edexcel and Pre-U specifications all include K_p, the equilibrium constant in terms of partial pressure.

The definition of the equilibrium constant for homogeneous gas-phase reactions has been misrepresented in A level for years. It is time that this is recognised and corrected with calculations of the Gibbs function ΔG from equilibrium constants now appearing in A level work. If exam boards are intent on making the standard pressure 100 kN m ^{– 2}  or 100 kPa, as has been recommended by IUPAC to replace the previous value of
1 atm,  then the consequence is that the equilibrium constant K_p must be defined correctly.

K_p is used for gas mixtures. Equilibrium constants in terms of concentration, K_c , are not affected in quite the same way because the standard state for a solution has not been changed from 1 mol dm ^{– 3}. There is a point to be made later about units, however.

 K_p: Homogeneous gaseous equilibria.

Consider the gaseous equilibrium

The equilibrium constant K_p is generally defined thus:

where p(A), p(B) and p(C) are the equilibrium partial pressures of the three gases.

If this is the expression which is to be used, then the partial pressures must be in atmospheres. If they are not then the numerical value of K_p will be wrong.

The definition of  K_p comes from thermodynamic arguments which it is not appropriate to give here. However the values p(A), p(B) and p(C) are not quite what they seem. In the words of a definitive text, Denbigh (1971 - full reference below):

 “ It is convenient to choose p₀ as unity, in the same units as p.” (Denbigh p.111)

 “ The standard pressure p₀ has been taken as unity and has not therefore been included explicitly in the equilibrium constant; in fact each p in K_p is really a ratio p/p₀ .” (Denbigh p.141)

 They are pressures compared with the standard state for a perfect gas, that is of the form p(X)/p₀(X) where p₀(X) is the standard pressure of the gas. The correct and complete expression for K_p is therefore:

It will be immediately clear that if all the p₀(X) are 1 atm then there is no numerical effect on the value
of K_p.

Since each term p(X)/p₀(X) is a ratio of two pressures, it is a number. This means that K_p has no units, since all the terms on the right are numbers - which will surprise many of you who have been asked to calculate K_p’s units in examination questions. K_p is a number.

The use of 1 atm as the standard pressure simplifies the expression for K_p but has unfortunately led to the belief that it has (or can have) units; initially the 1 atm was omitted but understood, and now is often forgotten.

One of the uses of K_p is to calculate the Gibbs free energy change through the expression

The logarithm function operates on numbers only; it does not operate on physical quantities. Therefore K_p must be a number, not some value with units such as atm ^{– 1} . To make K_p a number requires that the standard pressure be included in the K_p expression.

Examples using different values for the standard pressure.

Consider the homogeneous gaseous equilibrium already mentioned:

1 With a standard pressure of 1 atm.

Let us assume that the equilibrium partial pressures are p(A) = 2 atm, p(B) = 3 atm and p(C) = 2 atm. The standard A level text will have it that

 But we must include the standard state pressure to get the true equilibrium constant:

 This gives the number which we can use to calculate the free energy change G. At 298 K we obtain:

The value of ln (1/3) is – 1.1, so ΔG = + 2.72 kJ mol ^{– 1} .

2 With a standard pressure of 100 kN m ^{– 2} or 100 kPa.

The equilibrium partial pressures are now, for the same system as above, p(A) = 200 kPa, p(B) = 300 kPa and p(C) = 200 kPa. If you write an expression for K_p without including the standard pressure you will not get the true value ; note the ‘not equal to’ symbol!

This would obviously not give the same value for ΔG as in the first example above.

We must include the standard state pressure to get the true equilibrium constant:

This gives the same answers for K_p and ΔG as in example 1.

If the standard pressure is to be taken as 100 kPa, as it is in all AS level specifications where the standard state is being discussed, then any calculation of K_p at A2 must involve it if the correct result is to be achieved - unless for this purpose only a standard pressure of 1 atm is adopted.

The equilibrium constant in terms of concentration, K_c

The situation is the same here in that the concentrations used in the expression for K_c should all be divided by the standard state concentration, which is 1 mol dm -3. This does not change the numerical value but again it gives a number, as it must do if the logarithm function is to be applied to it.

Reference

Denbigh, KG, ‘The Principles of Chemical Equilibrium’. Cambridge University Press, 3^rd ed. 1971.